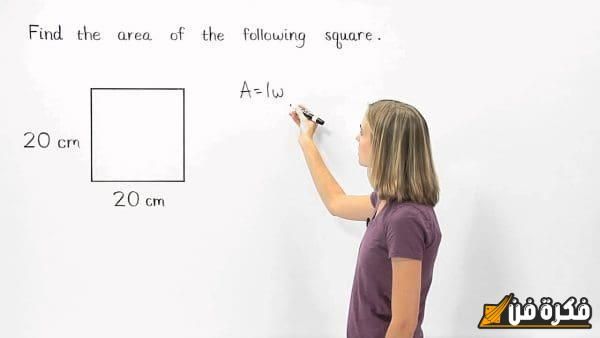
تعد مساحة المربع من المواضيع الأساسية في الرياضيات وعلم الهندسة، حيث إن المربع هو أحد الأشكال الهندسية الأكثر بغيتها وفهمًا،يمتاز المربع بأربعة أضلاع متساوية الطول، وأربع زوايا قائمة، الأمر الذي يجعله واحدًا من الأشكال الهندسية المثالية،ولأن المربع يتضمن العديد من الخصائص الهندسية، فإنه يُستخدم في العديد من التطبيقات العملية في مجالات مختلفة مثل العمارة، التصميم، الحرف اليدوية، وغيرها،ولهذا، فإن فهم كيفية حساب مساحة المربع يعد ذو أهمية قصوى في العديد من الأنشطة اليومية والدراسية.

ما هي مساحة المربع

تعتبر مساحة المربع مفهومًا رياضيًا مهمًا ويستند إلى بعض القوانين الأساسية،إذ يمكن قياس هذه المساحة عن طريق معرفة طول ضلع المربع، والذي يعد العنصر الأساسي لحساب المساحة.ämän يتفاوت استخدام هذه القوانين بين التعليم الأكاديمي والتطبيقات العملية استخدام القوانين الرياضية يساعد الطلاب والمهندسين والمهتمين في فروع الرياضيات والهندسة على تحقيق النتائج الدقيقة.

هناك عدة قوانين لحساب مساحة المربع، سنستعرضها في الفقرات التالية.

القانون الأول

يتعلق القانون الأول بشكل رئيسي بمساحة المربع ويرتبط طرديًا بمساحة المستطيل، حيث يمكن التعبير عن
مساحة المربع = الطول × العرض
لكن بالنسبة للمربع، يعتبر الطول والعرض متساويين،هذه الصيغة تجعل من السهل حساب المساحة بدقة، مما يسهل على الممارسين والمستخدمين إجراء عمليات حسابية دقيقة.

القانون الثاني

وضمن هذا القانون، يمكن حساب مساحة المربع بالاعتماد على طول قطر المربع،وبصيغة رياضية تصبح

مساحة المربع = (مربع طول القطر) / 2
يعتمد هذا القانون على إدراك الفرد لطول القطر، وهو مهم بشكل خاص في التطبيقات الهندسية.

القانون الثالث

هذا القانون يعتمد على المحيط، حيث يعرف المحيط في المربع بأنه مجموع أطوال جوانبه
المحيط = 4 × طول الضلع
ويمكن استنتاج طول الضلع من المحيط وبالتالي استخدامه في حساب المساحة.

القانون الرابع

في إطار القانون الرابع، يمكن حساب المساحة بالاعتماد على طريقة حساب القطر، وذلك باستخدام المثلثات القائمة،حيث يتم حساب القطر وفقًا للصيغة
القطر = الجذر التربيعي (طول الضلع الأول)² + (طول الضلع الثاني)²
هذا يمثل أهمية كبيرة لفهم الأبعاد الرياضية وكيفية تطبيقها على المربع.

خصائص المربع

يمتاز المربع بخصائص فريدة تميزه عن الأشكال الأخرى،وفيما يلي أبرز هذه الخصائص

• تتساوى جميع الزوايا في المربع وتكون قائمة بمقدار 90 درجة، مما يؤدي إلى أن مجموع الزوايا في الشكل يساوي 360 درجة.
• يجعل هرمي الطول المتساوي والزوايا المتطابقة من المربع شكلاً متكاملاً وأنيقًا في معظم التصميمات.
• تتساوى جميع الأقطار، مما يجعل كل قطر يقسم المربع إلى مثلثين متطابقين بالمساحة.

العلاقة بين المربع والأشكال الأخرى

يساهم المربع في بعض العلاقات الهندسية مع الأشكال الأخرى،يمكن أن يكون مشابهًا للمستطيل، حيث تشترك الأشكال في الخصائص المتماثلة مثل أن جوانبها متوازية وأبعادها متساوية،كما أن المربع يتشابه مع المعين ومتوازي الأضلاع في جوانب معينة، ولكن يتميز المربع بأن كل ضلعه يُعتبر متساوي الطول.

تعريف خصائص قطر المربع

القطر هو إحدى عناصر المربع الهامة ويمثل القطعة المستقيمة التي تمتد بين الزوايا المتقابلة،وتتمثل خصائصه في

• تحافظ جميع الأقطار على الطول المتساوي، مما يجعلها مقسومة إلى جزئيين متساويين عند التقاطع.
• تُعطي الأقطار وظائف مهمة في تحديد المساحة والتوازن داخل الشكل.

أهمية معرفة مساحة المربع

تتجاوز أهمية حساب مساحة المربع أبعاد الرياضيات البسيطة وتساهم في دراسة الأشكال الهندسية ودورها في التخصصات العلمية المختلفة،بخلاف استخدامها في التطبيقات العملية، فإن مساحة المربع تُعتبر مدخلًا لفهم الأبعاد الأكثر تعقيدًا،فكما تعكس المعادلات البسيطة أهمية المربع، فإن تفاصيل الحسابات تمكن الفرد من استكشاف الطبيعة الرياضية للأشكال المعقدة الأخرى.

في النهاية، يُظهر كافة المعلومات المتعلقة بمساحة المربع أن هذا المفهوم لا يقتصر فقط على التعلم الأكاديمي، بل يمتد ليشمل التطبيقات العملية في الحياة اليومية،بالتالي، يعتبر فهم كيفية حساب مساحة المربع أمرًا ضروريًا لتحقيق نتائج دقيقة وفعّالة في شتى المجالات.